Short-term forecasting of building heating load based on MVMD-SSA-LSTM

Authors

  • Bo Zhou School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China
  • Yueyi Zhang School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China
  • Chaoyang Fei School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China
  • Xiuming Li School of Metallurgy, Northeastern University, Shenyang 110819, China
  • Zhigang Xie School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China
  • Daohe Li School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China
Article ID: 297
660 Views

DOI:

https://doi.org/10.18686/cest297

Keywords:

building heating load forecast; multivariate variational mode decomposition; long short-term memory neural networks; sparrow search algorithm

Abstract

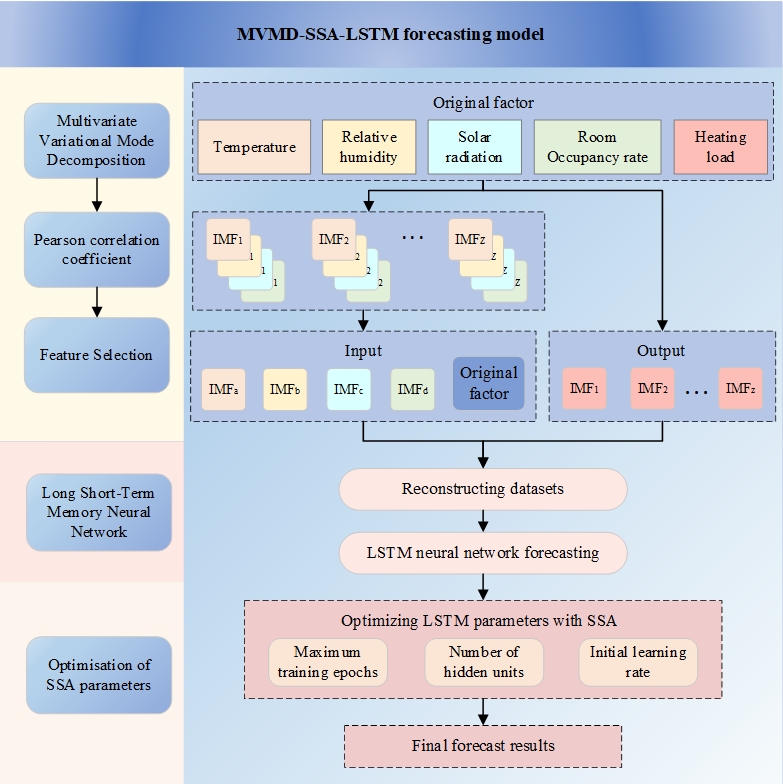
A short-term heating load forecast for buildings is a critical step in the subsequent control of energy systems, directly impacting system energy consumption. However, given that heating load and its influencing factors constitute volatile time series data, noise interference within the data significantly limits prediction accuracy and stability. To address this issue, this paper proposes a novel MVMD-SSA-LSTM model for building heating load forecasts, which integrates Multivariate Variational Mode Decomposition (MVMD), Sparrow Search Algorithm (SSA), and Long Short-Term Memory (LSTM) neural networks. Initially, a correlation analysis of the factors influencing building heating load is conducted to identify the key determinants. Subsequently, MVMD is employed to decompose the multidimensional dataset into several modes. A correlation analysis is then performed on these decomposed modes to extract supplementary features, which are combined with the original data to form a new dataset, thereby reducing feature redundancy. Finally, an LSTM neural network is utilized as the core predictive model, with the SSA algorithm optimizing three critical parameters: The maximum training iterations, the number of hidden units, and the initial learning rate. The predicted outputs of each heating load mode are aggregated to obtain the final forecast. Results demonstrate that the MVMD-SSA-LSTM model effectively mitigates the uncertainty in heating load sequence forecasts, overcoming noise disturbances and exhibiting superior performance compared to other commonly used models, with significantly higher accuracy and stability.

Downloads

Published

2025-03-05

How to Cite

Zhou, B., Zhang, Y., Fei, C., Li, X., Xie, Z., & Li, D. (2025). Short-term forecasting of building heating load based on MVMD-SSA-LSTM. Clean Energy Science and Technology, 3(1), 297. https://doi.org/10.18686/cest297

Issue

Vol. 3 No. 1 (2025): Advanced Technologies in Smart and Sustainable Energy for Carbon Neutrality Transformations

Section

Article

License

Copyright (c) 2025 Author(s)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

References

1. Ekonomou L, Christodoulou CA, Mladenov V. A short-term load forecasting method using artificial neural networks and wavelet analysis. Int. J. Power Syst. 2016; 1: 64–68.

2. Verbeke S, Audenaert A. Thermal inertia in buildings: A review of impacts across climate and building use. Renewable and Sustainable Energy Reviews. 2018; 82: 2300–2318. DOI: https://doi.org/10.1016/j.rser.2017.08.083

3. Rugani R, Bigazzi M, Fantozzi F, et al. Impact of building thermal inertia in different climates using energy dynamic simulation through a simplified description model. In: Proceedings of the 17th IBPSA Conference; 1–3 September 2021; Bruges, Belgium. Volume 17, pp. 2578–2585. DOI: https://doi.org/10.26868/25222708.2021.30515

4. Wu Q, Wang J, Meng X. Influence of wall thermal performance on the contribution efficiency of the Phase-Change Material (PCM) layer. Case Studies in Thermal Engineering. 2021; 28: 101398. DOI: https://doi.org/10.1016/j.csite.2021.101398

5. Chapaloglou S, Varagnolo D, Marra F, et al. Data-driven energy management of isolated power systems under rapidly varying operating conditions. Applied Energy. 2022; 314: 118906. DOI: https://doi.org/10.1016/j.apenergy.2022.118906

6. Luo XJ, Oyedele LO. Forecasting building energy consumption: Adaptive long-short term memory neural networks driven by genetic algorithm. Advanced Engineering Informatics. 2021; 50: 101357. DOI: https://doi.org/10.1016/j.aei.2021.101357

7. Hu J, Zou Y, Soltanov N. A multilevel optimization approach for daily scheduling of combined heat and power units with integrated electrical and thermal storage. Expert Systems with Applications. 2024; 250: 123729. DOI: https://doi.org/10.1016/j.eswa.2024.123729

8. Wei S, Tien PW, Calautit JK, et al. Vision-based detection and prediction of equipment heat gains in commercial office buildings using a deep learning method. Applied Energy. 2020; 277: 115506. DOI: https://doi.org/10.1016/j.apenergy.2020.115506

9. Sze V, Chen YH, Yang TJ, et al. Efficient processing of deep neural networks: A tutorial and survey. Proceedings of the IEEE. 2017; 105(12): 2295–2329. DOI: https://doi.org/10.1109/JPROC.2017.2761740

10. Pan L, Wang S, Wang J, et al. Research on central air conditioning systems and an intelligent prediction model of building energy load. Energies. 2022; 15(24): 9295. DOI: https://doi.org/10.3390/en15249295

11. Yildiz B, Bilbao JI, Sproul AB. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renewable and Sustainable Energy Reviews. 2017; 73: 1104–1122. DOI: https://doi.org/10.1016/j.rser.2017.02.023

12. Wang Z, Hong T, Piette MA. Building thermal load prediction through shallow machine learning and deep learning. Applied Energy. 2020; 263: 114683. DOI: https://doi.org/10.1016/j.apenergy.2020.114683

13. Zhou C, Fang Z, Xu X, et al. Using long short-term memory networks to predict energy consumption of air-conditioning systems. Sustainable Cities and Society. 2020; 55: 102000. DOI: https://doi.org/10.1016/j.scs.2019.102000

14. Xu Y, Gao W, Qian F, et al. Potential analysis of the attention-based LSTM model in ultra-short-term forecasting of building HVAC energy consumption. Frontiers in Energy Research. 2021; 9: 730640. DOI: https://doi.org/10.3389/fenrg.2021.730640

15. Chalapathy R, Khoa NLD, Sethuvenkatraman S. Comparing multi-step ahead building cooling load prediction using shallow machine learning and deep learning models. Sustainable Energy, Grids and Networks. 2021; 28: 100543. DOI: https://doi.org/10.1016/j.segan.2021.100543

16. Yu Y, Si X, Hu C, et al. A review of recurrent neural networks: LSTM cells and network architectures. Neural computation. 2019; 31(7): 1235–1270. DOI: https://doi.org/10.1162/neco_a_01199

17. Zhang L, Wen J, Li Y, et al. A review of machine learning in building load prediction. Applied Energy. 2021; 285: 116452. DOI: https://doi.org/10.1016/j.apenergy.2021.116452

18. Das A, Annaqeeb MK, Azar E, et al. Occupant-centric miscellaneous electric loads prediction in buildings using state-of-the-art deep learning methods. Applied Energy. 2020; 269: 115135. DOI: https://doi.org/10.1016/j.apenergy.2020.115135

19. Xue J, Shen B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering. 2020; 8(1): 22–34. DOI: https://doi.org/10.1080/21642583.2019.1708830

20. Saafan MM, El-Gendy EM. IWOSSA: An improved whale optimization salp swarm algorithm for solving optimization problems. Expert Systems with Applications. 2021; 176: 114901. DOI: https://doi.org/10.1016/j.eswa.2021.114901

21. An W, Gao B, Liu J, et al. Predicting hourly heating load in residential buildings using a hybrid SSA–CNN–SVM approach. Case Studies in Thermal Engineering. 2024; 59: 104516. DOI: https://doi.org/10.1016/j.csite.2024.104516

22. Madiniyeti J, Chao Y, Li T, et al. Concrete dam deformation prediction model research based on SSA–LSTM. Applied Sciences. 2023; 13(13): 7375. DOI: https://doi.org/10.3390/app13137375

23. Huang Z, Huang J, Min J. SSA-LSTM: Short-Term photovoltaic power prediction based on feature matching. Energies. 2022; 15(20): 7806. DOI: https://doi.org/10.3390/en15207806

24. Gao X, Guo W, Mei C, et al. Short-term wind power forecasting based on SSA-VMD-LSTM. Energy Reports. 2023; 9: 335–344. DOI: https://doi.org/10.1016/j.egyr.2023.05.181

25. Han M, Zhong J, Sang P, et al. A combined model incorporating improved SSA and LSTM algorithms for short-term load forecasting. Electronics. 2022; 11(12): 1835. DOI: https://doi.org/10.3390/electronics11121835

26. Chen H, Zhang H, Wu S, et al. Numerical simulation and optimisation design for ventilation and heat dissipation in high-temperature and high-load indoor substations. Case Studies in Thermal Engineering. 2024; 59: 104502. DOI: https://doi.org/10.1016/j.csite.2024.104502

27. Cha YJ, Mostafavi A, Benipal SS. DNoiseNet: Deep learning-based feedback active noise control in various noisy environments. Engineering Applications of Artificial Intelligence. 2023; 121: 105971. DOI: https://doi.org/10.1016/j.engappai.2023.105971

28. Genzel M, Macdonald J, März M. Solving inverse problems with deep neural networks–robustness included? IEEE Transactions on Pattern Analysis and Machine Intelligence. 2022; 45(1): 1119–1134. DOI: https://doi.org/10.1109/TPAMI.2022.3148324

29. Leprince J, Madsen H, Miller C, et al. Fifty shades of grey: Automated stochastic model identification of building heat dynamics. Energy and Buildings. 2022; 266: 112095. DOI: https://doi.org/10.1016/j.enbuild.2022.112095

30. Bampoulas A, Pallonetto F, Mangina E, et al. A Bayesian deep-learning framework for assessing the energy flexibility of residential buildings with multicomponent energy systems. Applied Energy. 2023; 348: 121576. DOI: https://doi.org/10.1016/j.apenergy.2023.121576

31. Yeh JR, Shieh JS, Huang NE. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Advances in Adaptive Data Analysis. 2010; 2(02): 135–156. DOI: https://doi.org/10.1142/S1793536910000422

32. Wang H, Huang S, Li P, et al. An improved wavelet transform threshold method for denoising fault signals. Measurement Science and Technology. 2016; 27(3): 1–10.

33. Liu H, Wang W, Xiang C, et al. A de-noising method using the improved wavelet threshold function based on noise variance estimation. Mechanical Systems and Signal Processing. 2018; 99: 30–46. DOI: https://doi.org/10.1016/j.ymssp.2017.05.034

34. Wardana ANI. A comparative study of EMD, EWT and VMD for detecting the oscillation in control loop. In: Proceedings of the 2016 International Seminar on Application for Technology of Information and Communication (ISemantic); 05–06 August 2016; Semarang, Indonesia. DOI: https://doi.org/10.1109/ISEMANTIC.2016.7873810

35. Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Transactions on Signal Processing. 2014; 62(3): 531–544. DOI: https://doi.org/10.1109/TSP.2013.2288675

36. Fu J, Cai F, Guo Y, et al. An Improved VMD‐Based Denoising Method for Time Domain Load Signal Combining Wavelet with Singular Spectrum Analysis. Mathematical Problems in Engineering. 2020; 2020(1): 1485937. DOI: https://doi.org/10.1155/2020/1485937

37. Bagheri A, Ozbulut OE, Harris DK. Structural system identification based on variational mode decomposition. Journal of Sound and Vibration. 2018; 417: 182–197. DOI: https://doi.org/10.1016/j.jsv.2017.12.014

38. ur Rehman N, Aftab H. Multivariate variational mode decomposition. IEEE Transactions on signal processing. 2019; 67(23): 6039–6052. DOI: https://doi.org/10.1109/TSP.2019.2951223

39. Zhang L, Li J, Xu X, et al. High spatial granularity residential heating load forecast based on Dendrite net model. Energy. 2023; 269: 126787. DOI: https://doi.org/10.1016/j.energy.2023.126787

40. Salami BA, Abba SI, Adewumi AA, et al. Building energy loads prediction using bayesian-based metaheuristic optimized-explainable tree-based model. Case Studies in Construction Materials. 2023; 19: e02676. DOI: https://doi.org/10.1016/j.cscm.2023.e02676

41. Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D: Nonlinear Phenomena. 2020; 404: 132306. DOI: https://doi.org/10.1016/j.physd.2019.132306

42. Awadallah M A, Al-Betar M A, Doush I A, et al. Recent versions and applications of sparrow search algorith. Archives of Computational Methods in Engineering, 2023, 30(5): 2831-2858. DOI: https://doi.org/10.1007/s11831-023-09887-z

43. Asuero AG, Sayago A, González AG. The correlation coefficient: An overview. Critical Reviews in Analytical Chemistry. 2006; 36(1): 41–59. DOI: https://doi.org/10.1080/10408340500526766